Vibrations

Exercice constante de phase

Déterminer l'amplitude et la constante de phase si ...

exemple  

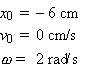
Exercice masse 2 kg

a = - 96p² cos( 4pt + p/6) m/s²

Solution

Exercice masse 2 kg

v = 32p cos( 4pt + p/6) m/s

Solution

Tracé de     courbes      MHS         

x = 8 cos (9pt + p/6) cm

Déterminez l’amplitude, la période, la constante de phase, la vitesse initiale, la position initiale de ce mouvement oscillatoire. Faites une représentation graphique de sa position x en fonction du temps t.

Solution

Exercice x=1 cm

Un objet exécute un mouvement harmonique simple de fréquence 1/p Hz avec une amplitude de 2 cm.

a) Lorsque l’objet est à 1 cm de sa position d’équilibre, déterminez la valeur absolue de sa vitesse.

b) Déterminez sa vitesse maximale durant l’oscillation.

Solution

  Exercice  MHA

Soit une masse de 500 g qui est suspendue à l'extrémité d'un ressort de constante d'élasticité égale à 34 N/m.

Voici un graphique approximatif de la position (x) de la masse en fonction du temps (t). (Les valeurs indiquées sont toutefois précises.)

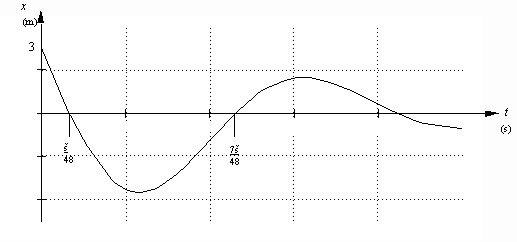
Déterminez complètement l'équation de la position en fonction du temps.

Solution

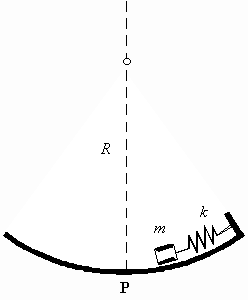
Exercice surface sphérique et ressort

Soit une masse m attachée à un ressort de constante k qui oscille sur une surface sphérique de rayon R ....

  Solution

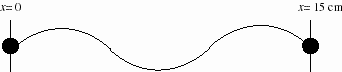
Exercice onde harmonique

Onde harmonique

Soit une onde harmonique d’amplitude 2 cm dont la longueur d’onde est de 10 cm .La vitesse de propagation est de 40 cm/s vers la droite. Si y = 0 à x = 0 et à t = 0 et que la vitesse transversale est alors positive, déterminez complètement l’équation de l’onde y(x,t).

Représentez cette onde à t=0 puis à t=1/8 s .

Solution

Exercice

Niveau acoustique

Niveau acoustique

Deux petits haut-parleurs ( considérés comme des sources ponctuelles) émettent un signal acoustique de fréquence égale à 1000 Hz avec une puissance efficace de 5,0 Watt sans distorsion dans un milieu sans bruit de fond. Les deux haut-parleurs sont placés l’un à côté de l’autre. Déterminez le niveau acoustique à une distance de 10,0 m des haut-parleurs dans les situations suivantes :

a) un seul haut-parleur est en opération

b) les deux haut-parleurs sont en opération.

c) les deux haut-parleurs sont en opération et on double la puissance de chacun.

Solution

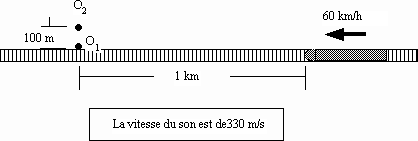
Exercice effet Doppler et train

.

Exercice effet Doppler et haut-parleur

       Effet Doppler

Solution

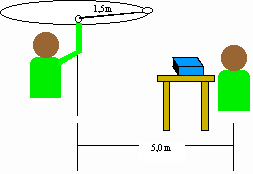
Réponses:

a) 1 061 Hz

b) 946 Hz

Exercice corde vibrante

Exercice sur le spectre d'un son

Spectre d’un son

Considérez  une onde acoustique décrite par l’équation de déplacement suivante :

   s(t) = s_m   [A₁ sin (wt) + A₂ sin (2wt) + A₃ sin (3wt) + A₄ sin (4wt) ]

dans laquelle w =2pf et la fréquence f vaut 1000 Hz.

En vous servant d’un chiffrier électronique (Excel par exemple), tracez la courbe représentative de cette onde s en fonction du temps t  (pour t compris entre 0 et 3 ms) en utilisant les coefficients suivants selon le dernier chiffre de votre numéro matricule.

Solution de Sophie Talbot

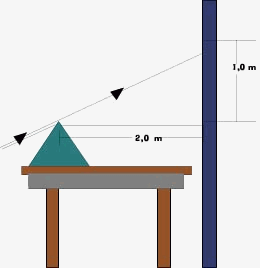
Prisme sur la table

Prisme

 On dirige un faisceau laser sur un prisme équiangle déposé sur une table horizontale. Une partie du faisceau frôle le sommet du prisme et l'autre partie traverse le prisme et en ressort parallèle à la surface de la table. Les deux spots lumineux obtenus sur le mur situé à 2,0 m du sommet du prisme sont espacés de 1,0 m. Déterminez la valeur de l'indice de réfraction du prisme.