Exercice

Onde harmonique

Soit une onde harmonique d’amplitude 2 cm dont la longueur d’onde est de 10 cm .La vitesse de propagation est de 40 cm/s vers la droite. Si y = 0 à x = 0 et à t = 0 et que la vitesse transversale est alors positive, déterminez complètement l’équation de l’onde y(x,t).

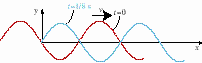
Représentez cette onde à t=0 puis à t=1/8 s .

Solution :

Écrivons d’abord l’équation générale de l’onde harmonique qui voyage vers la droite soit

dans laquelle

alors

et

Le plus difficile est de déterminer la constante de phase à l’aide des conditions initiales :

ce qui donne comme possibilités :

Il faut choisir entre les deux à l’aide de la vitesse transversale qui est ici positive, soit :

ce qui admet comme solution :

alors l’équation complète de l’onde est :

Voici la représentation de l’onde à deux instants différents :

 Retour