Exercice
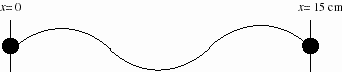
La figure précédente montre (à t= 0 s) une corde vibrante de masse linéique de 1g/m dont la fréquence du son émis est de 4 000 Hz.
a) Déterminez la tension dans la corde.
Selon le graphique ci-haut, la longueur d’onde est l = 10 cm = 0,1 m
On peut obtenir la vitesse de propagation selon : v = l f = 0,1 ´ 4 000 = 400 m/s
La vitesse de propagation dépend de la tension dans la corde car
![]()
b) Dessinez la forme de la corde à t = 3/16 000 s.
La vibration stationnaire peut être décrite par l’équation suivante : ![]()
Dans laquelle ![]()
Et alors pour t = 3/16 000 s, on obtient ![]()
Et ainsi y = 0 pour cet instant. La corde est alors droite.

