Le mouvement correspondant est un mouvement harmonique sous-amorti, ainsi son équation est :

Déterminons la pulsation naturelle :

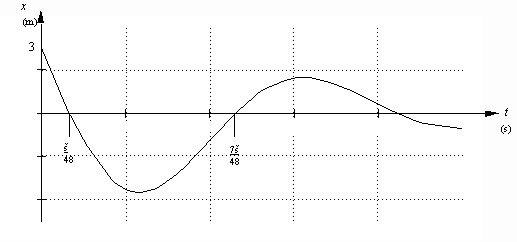
D’après le graphique, on constate que la demi-période est : mais alors w’=8 rad/s

On sait aussi que : ; ce qui devient

Alors, on obtient : g = 4 s^-1

Le graphique nous indique que le premier passage à x = 0 se produit à t = p/48 s.

Il faut alors que le cosinus soit nul pour la première fois,  ce qui exige que son argument soit de p/2.

Ainsi : ; ce qui donne

Pour déterminer la valeur de A_o, on se sert du point de départ : x_o = 3 m pour un temps t = 0.

; ce qui donne A_o = 6 m

Alors l’équation finale de la vibration est :

Retour